Summing the Multinomial Coefficients

The sum of binomial coefficients Image may be NSFW.
Clik here to view.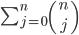 equals 2ⁿ, because Image may be NSFW.
Clik here to view.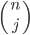 is the number of ways to pick j elements from a set of size n, and 2ⁿ is the size of the powerset, the set of all subsets, of a set of size n: the sum, over all subset sizes, of the number of ways to choose subsets of a given size, is equal to the number of subsets. You can also see this using the binomial theorem itself:

Image may be NSFW.
Clik here to view.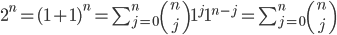

But of course there's nothing special about two; it works for multinomial coefficients just the same. The sum, over all m-tuples of subset sizes, of the number of ways to split a set of size n into subsets of sizes given by the m-tuple, is equal to the number of ways to split a set of size n into m subsets (viz., mⁿ).